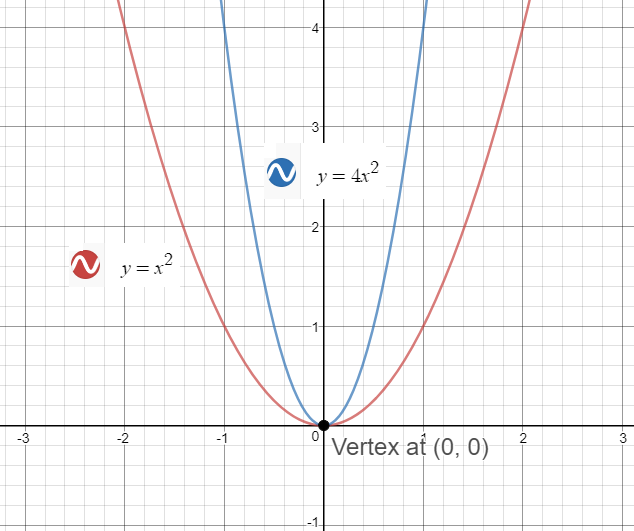
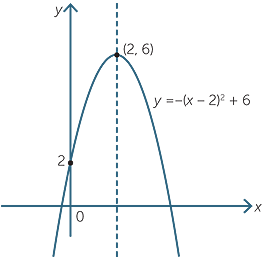
[最も好ましい] parabola y=x^2 1 y=19-(x)^2 279104
It has both Q Given y = 2 (x 5) 6, the vertex is Q Given 1/2 (x 4) 5, the equation of the axis of symmetry is Q A parabola has a vertex at (3,2)
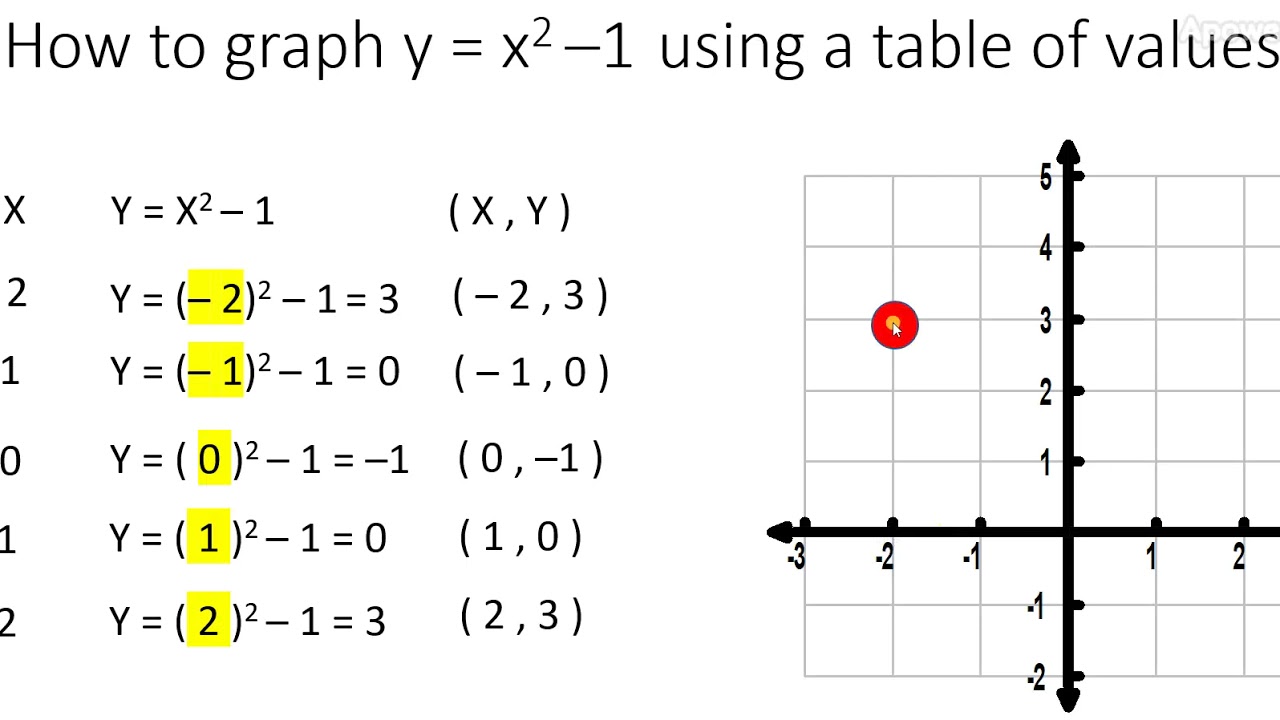
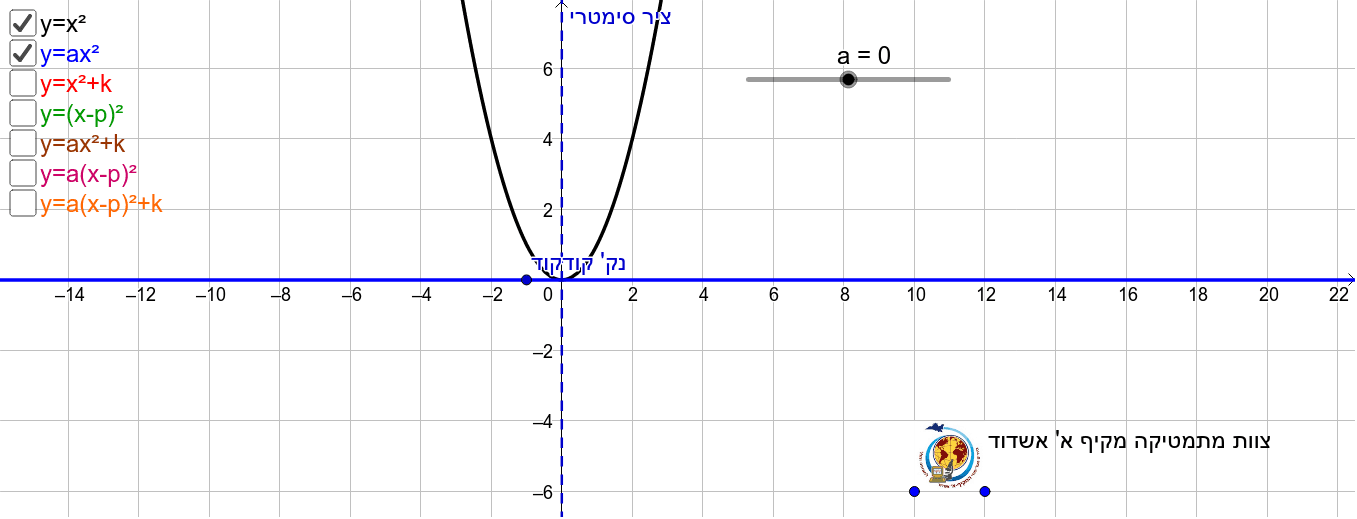
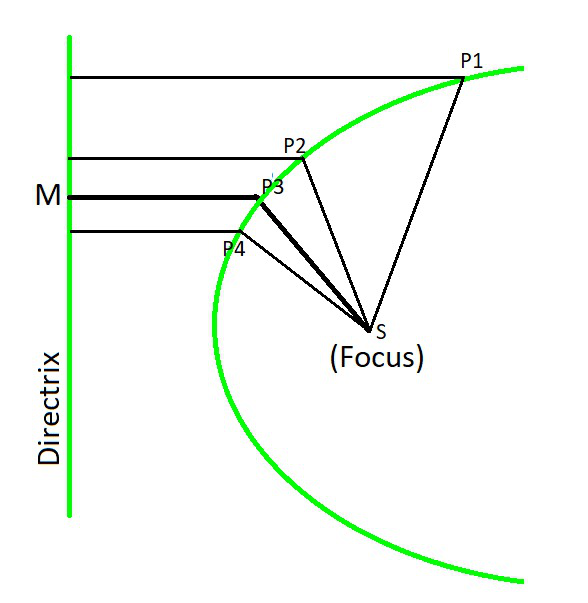
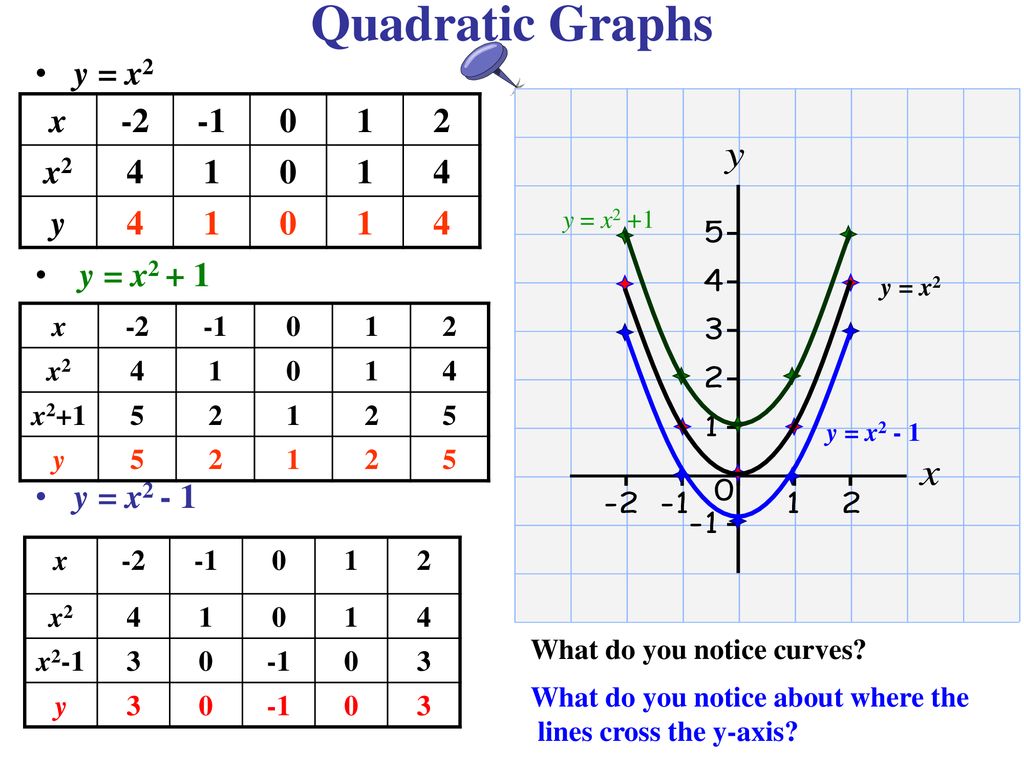
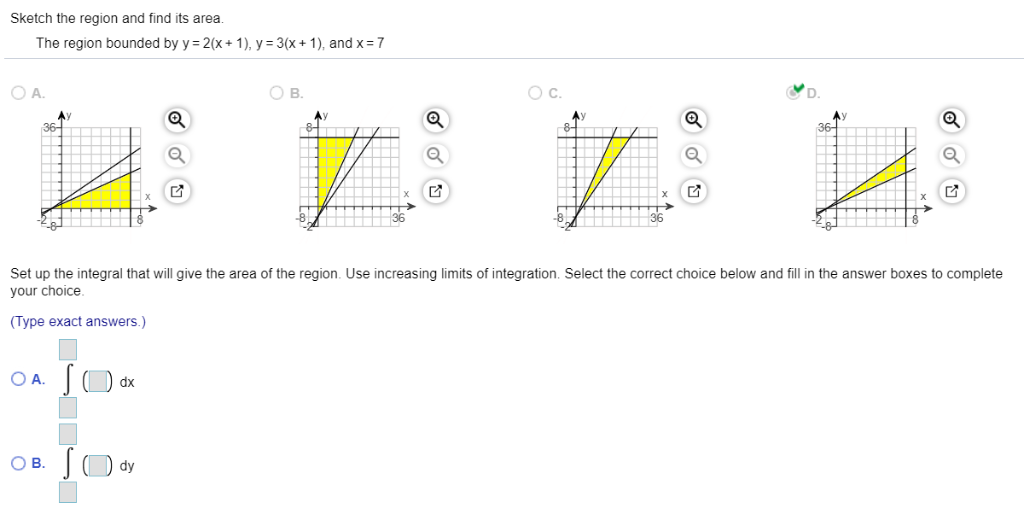
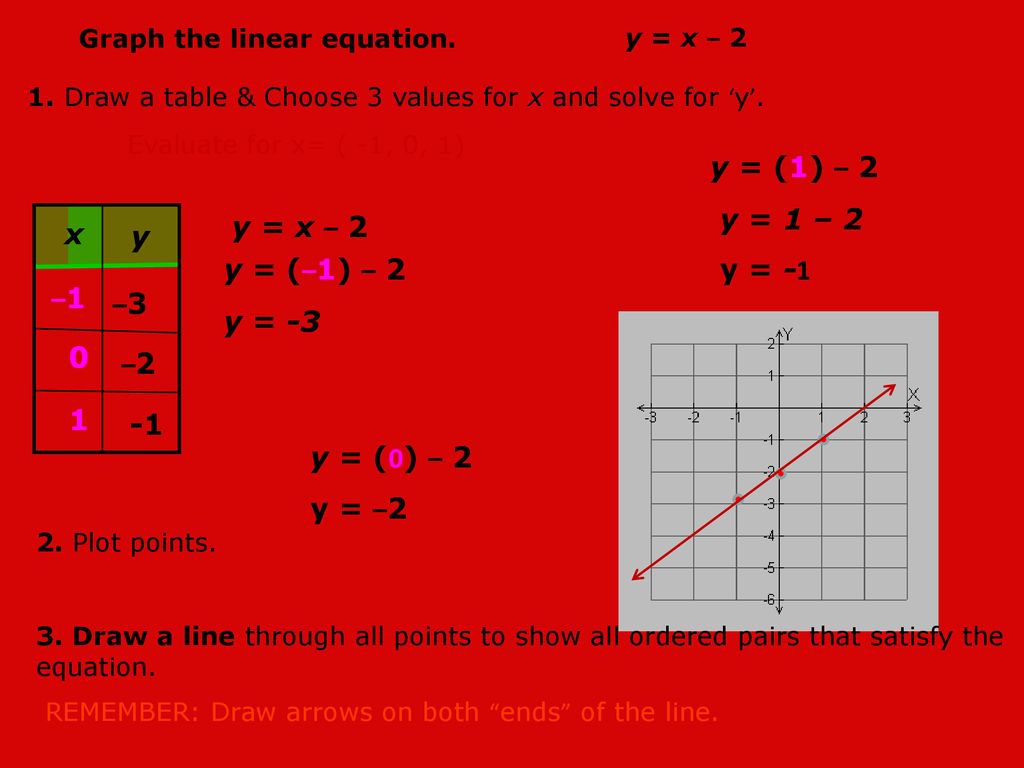
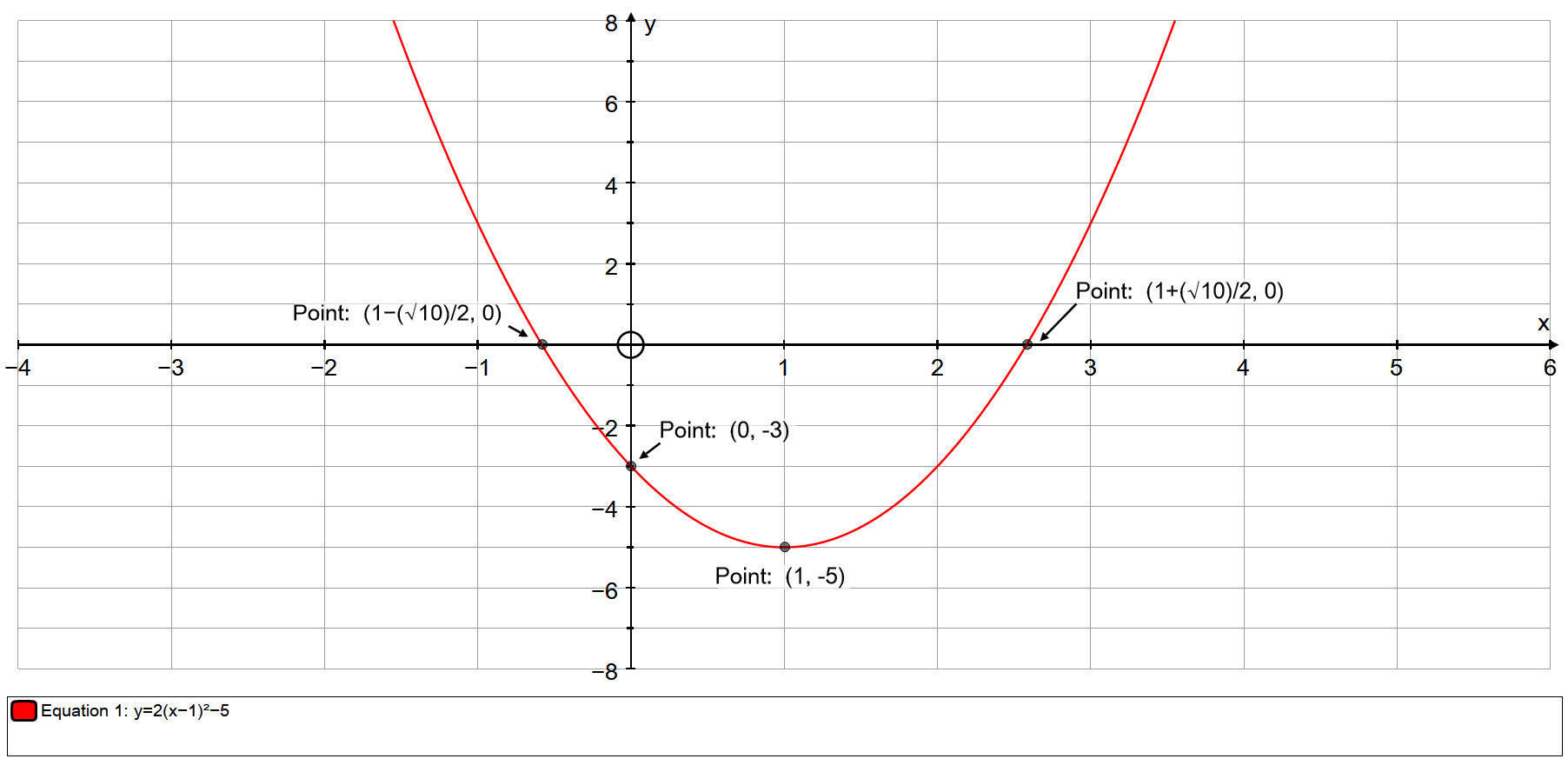
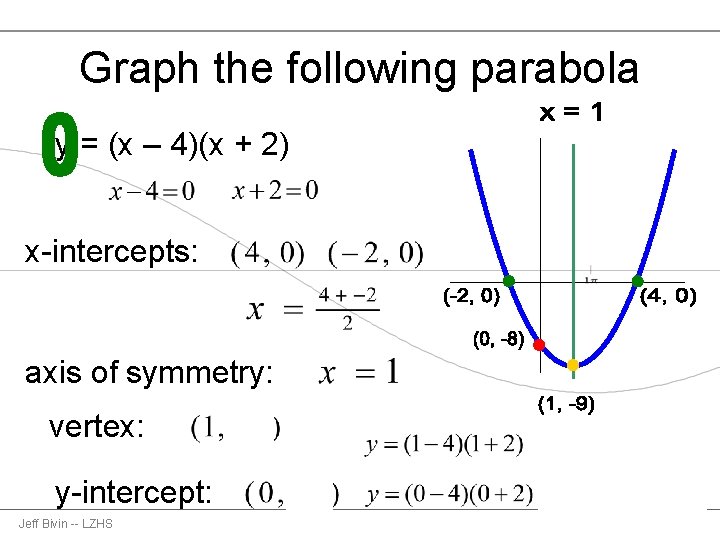
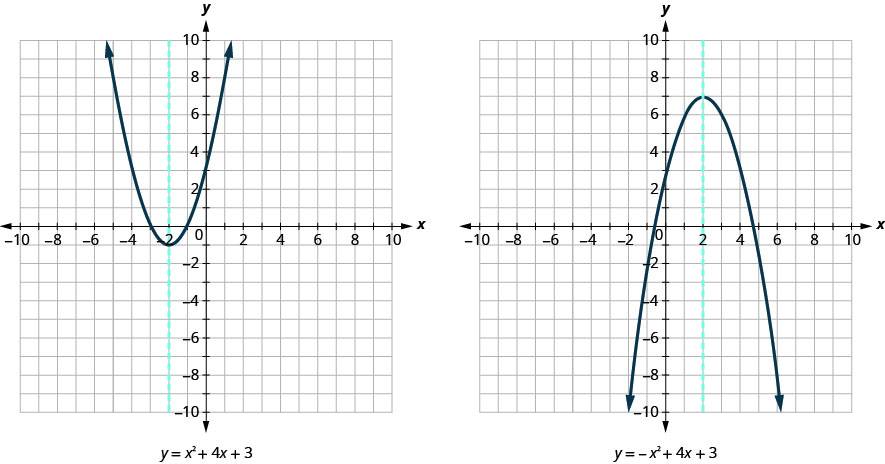
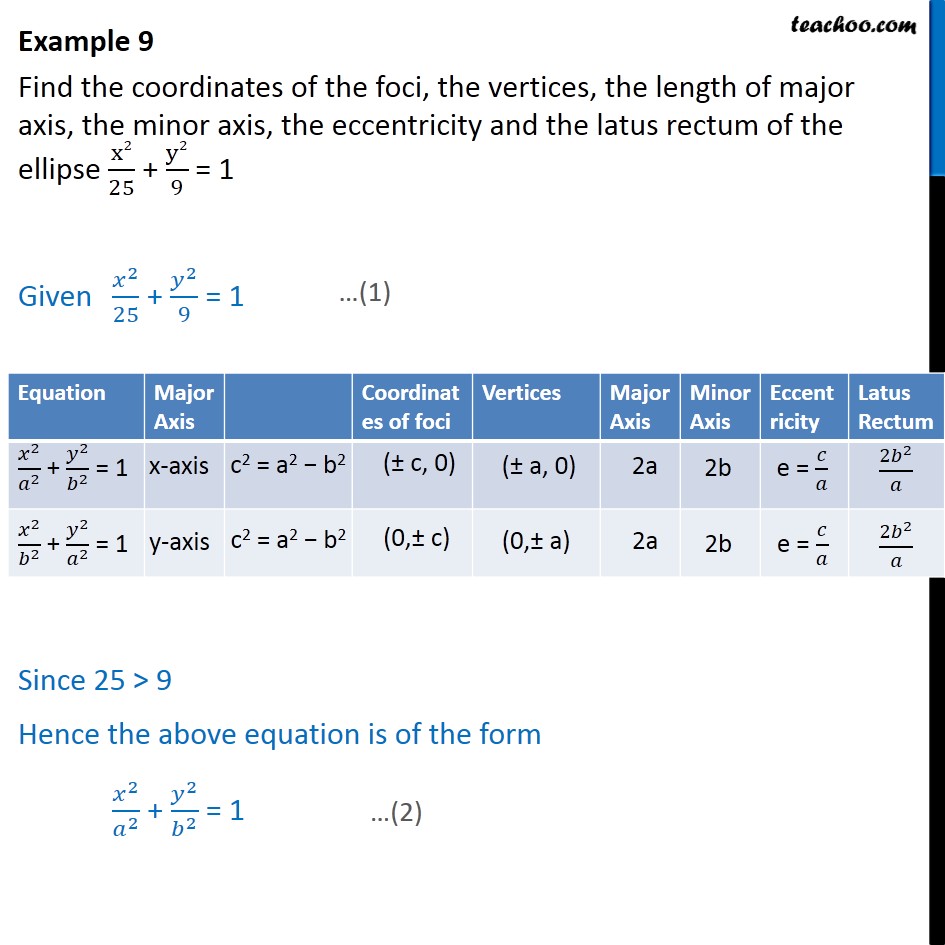
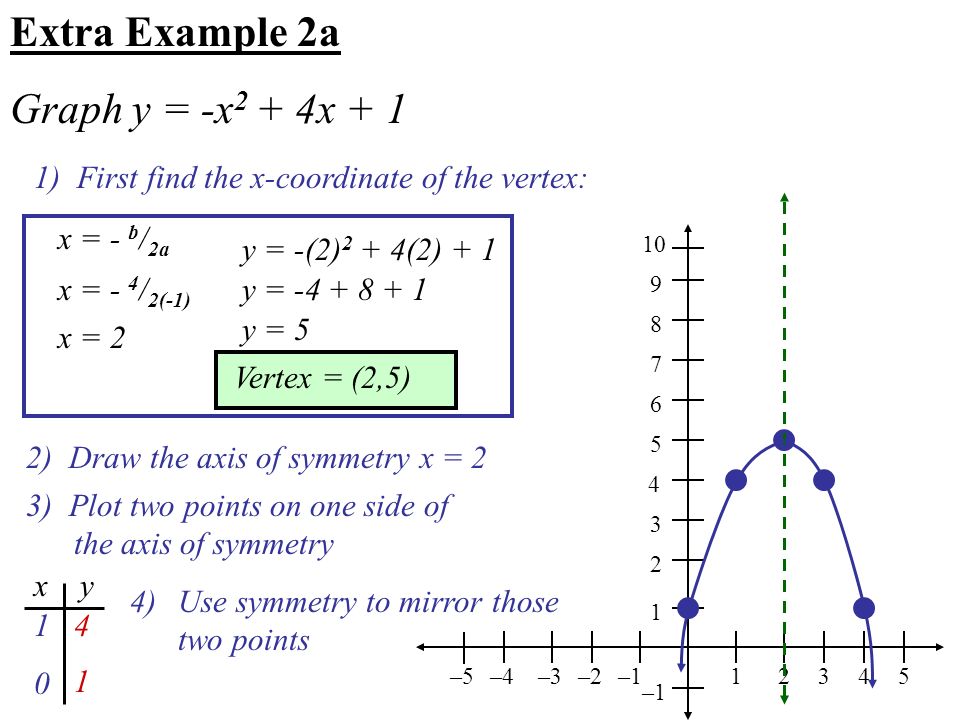
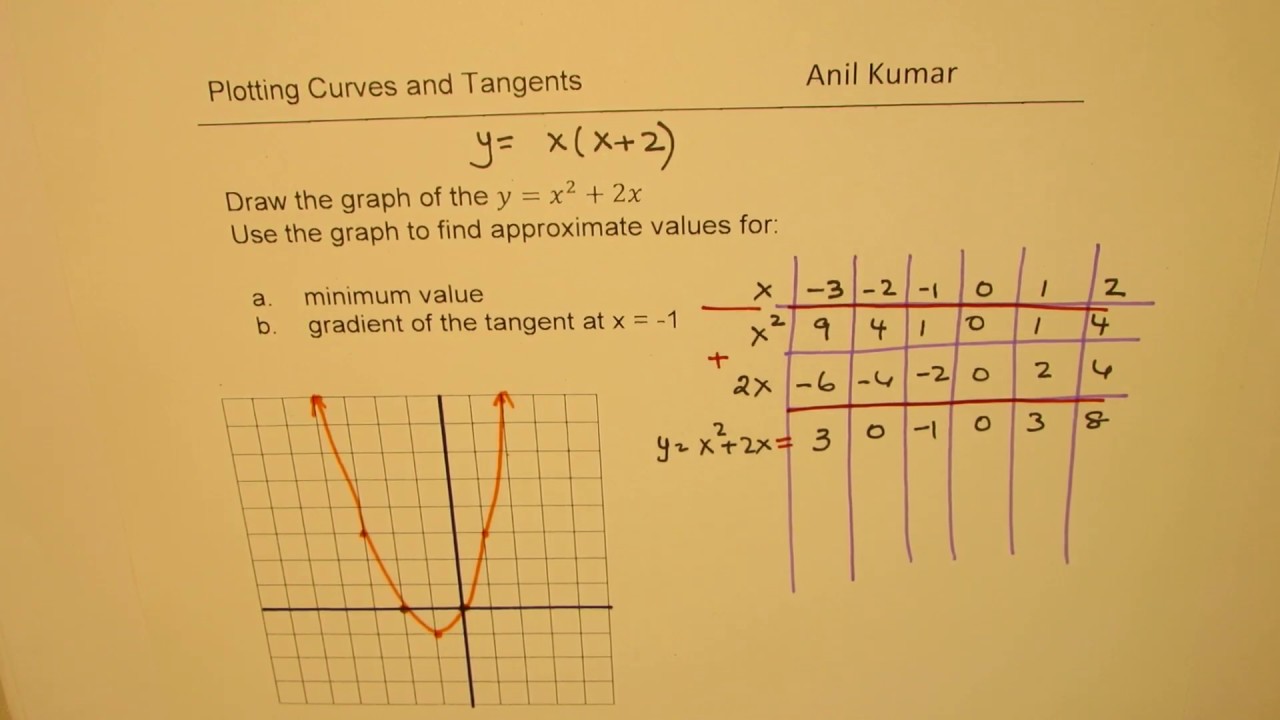
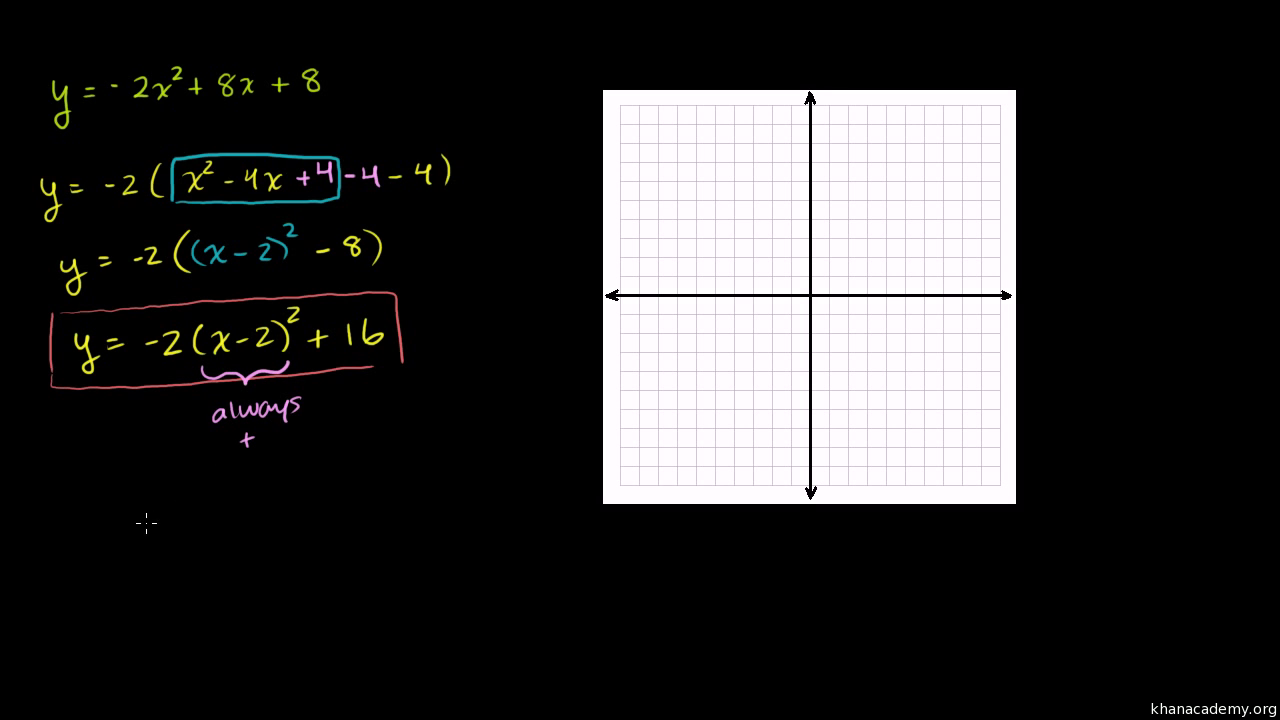
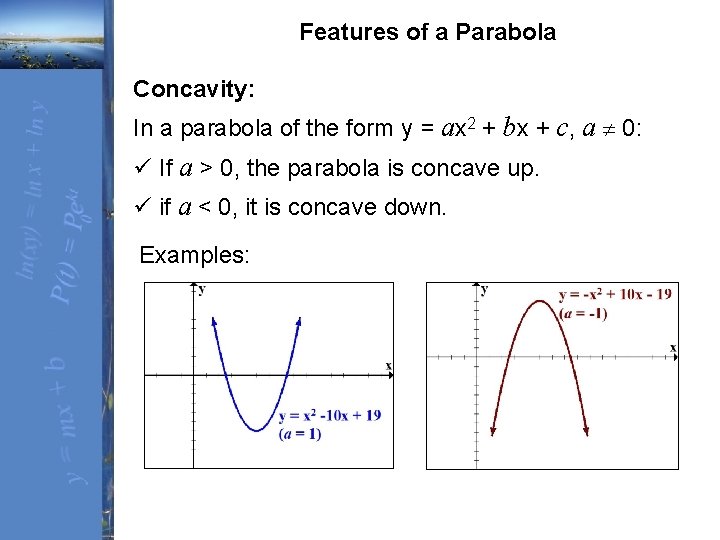
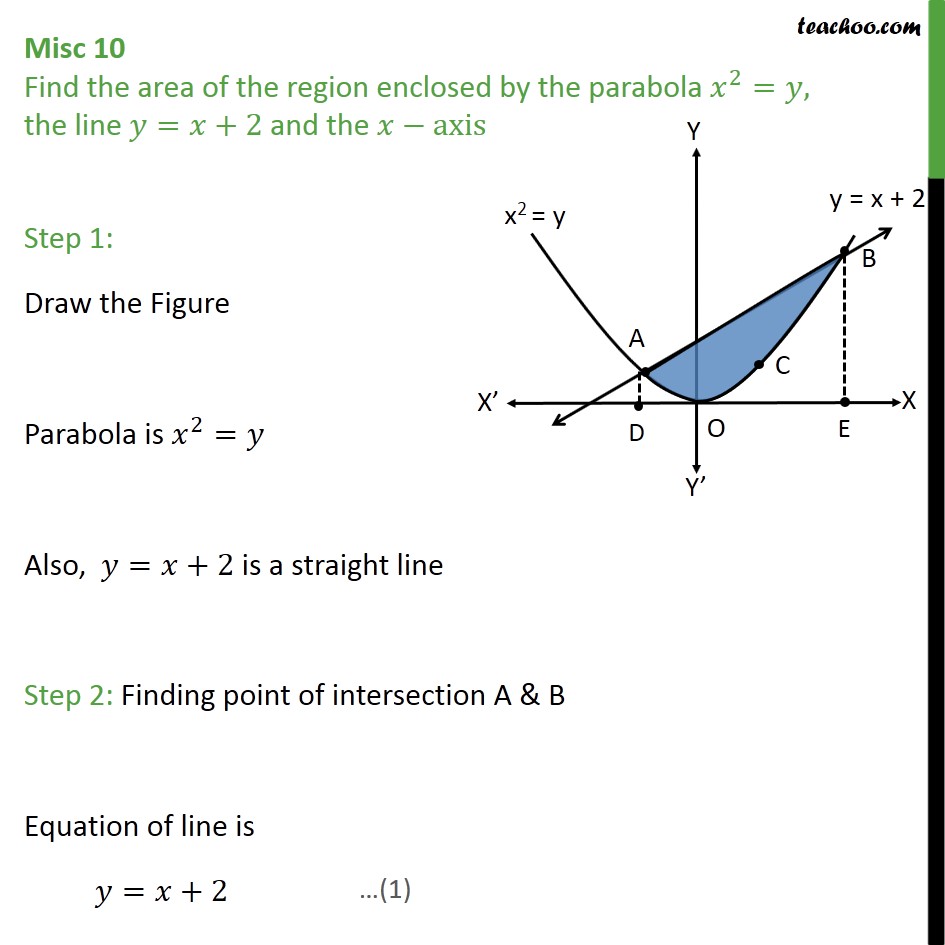
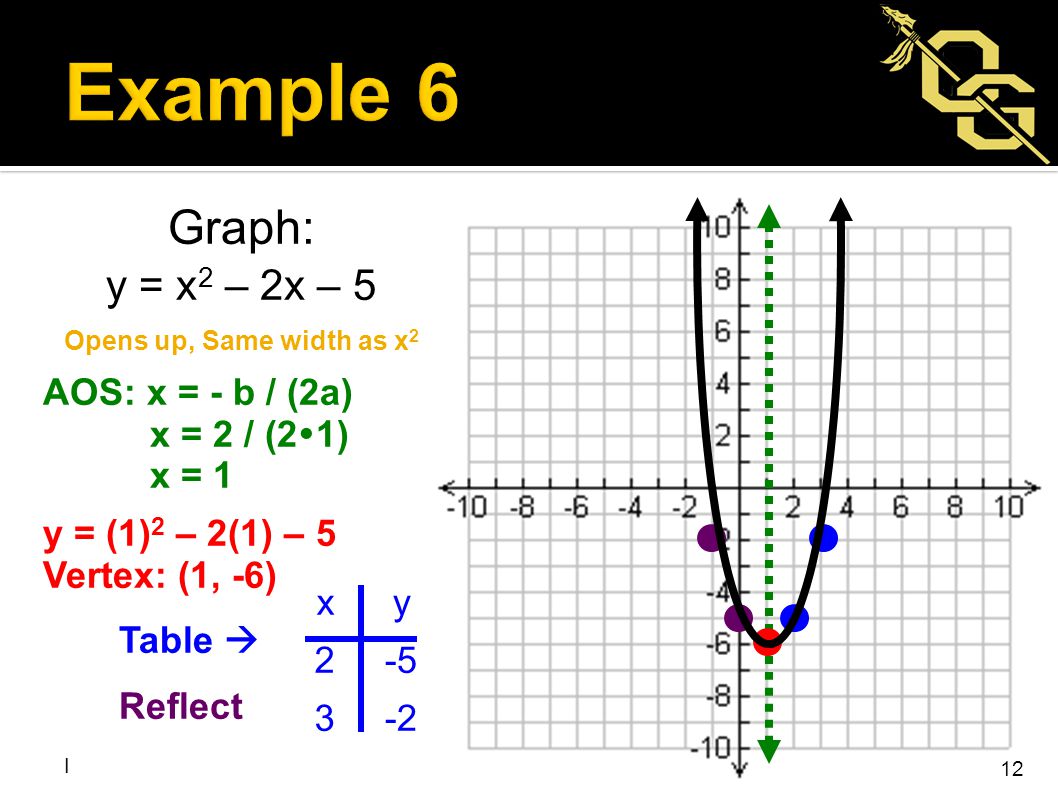
Parabola y=x^2 1 y=19-(x)^2-Each of the parabola you drew in (a) y = (x1)2 i) Detemuine the coordinate of the tuming points of each of the following quadratics Note that the value of is irrelevant Exercise #4 y = —2 (x —3)2 10 Again the ñnction y is shown below Graph each of the following more complicated quadratics V\ithout the use of your calculator The equation is (x 1 2)2 = 4(y −3) We compare this equation to the standard equation of the parabola (x −a)2 = 2p(x −b) p = 2 The vertex is V = (a,b) = ( − 1 2,3) The focus is F = (a,b p 2) = ( − 1 2,4) The directrix is y = b − p 2 = 3 −1 = 2
Parabola y=x^2 1 y=19-(x)^2のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | ||
 |  |  |
 |  | |
「Parabola y=x^2 1 y=19-(x)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
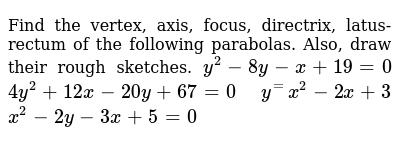 |  | |
 |  | |
 |  |  |
「Parabola y=x^2 1 y=19-(x)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
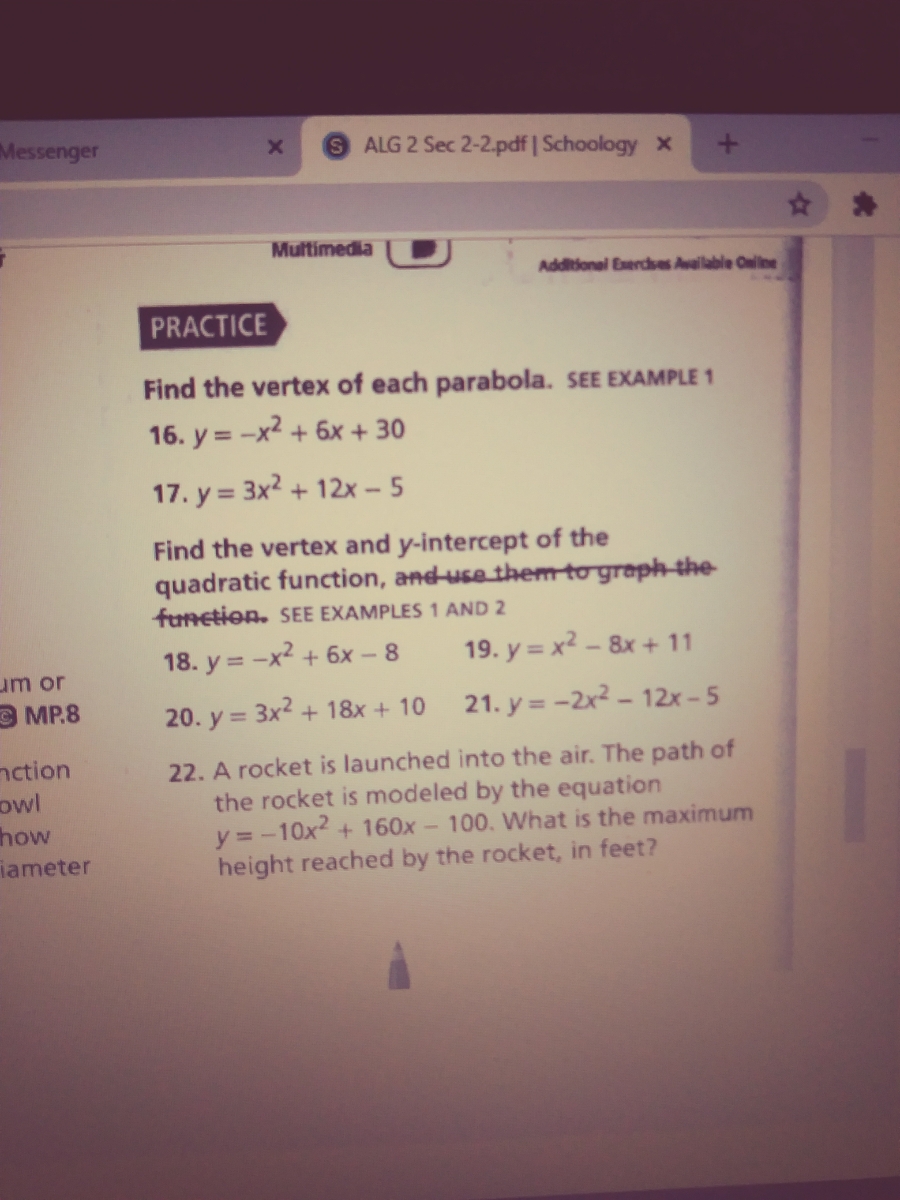
 | 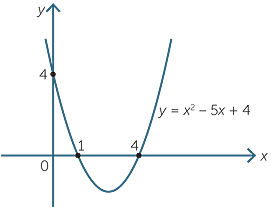 | |
 |  | |
「Parabola y=x^2 1 y=19-(x)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
 |  | |
「Parabola y=x^2 1 y=19-(x)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「Parabola y=x^2 1 y=19-(x)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | 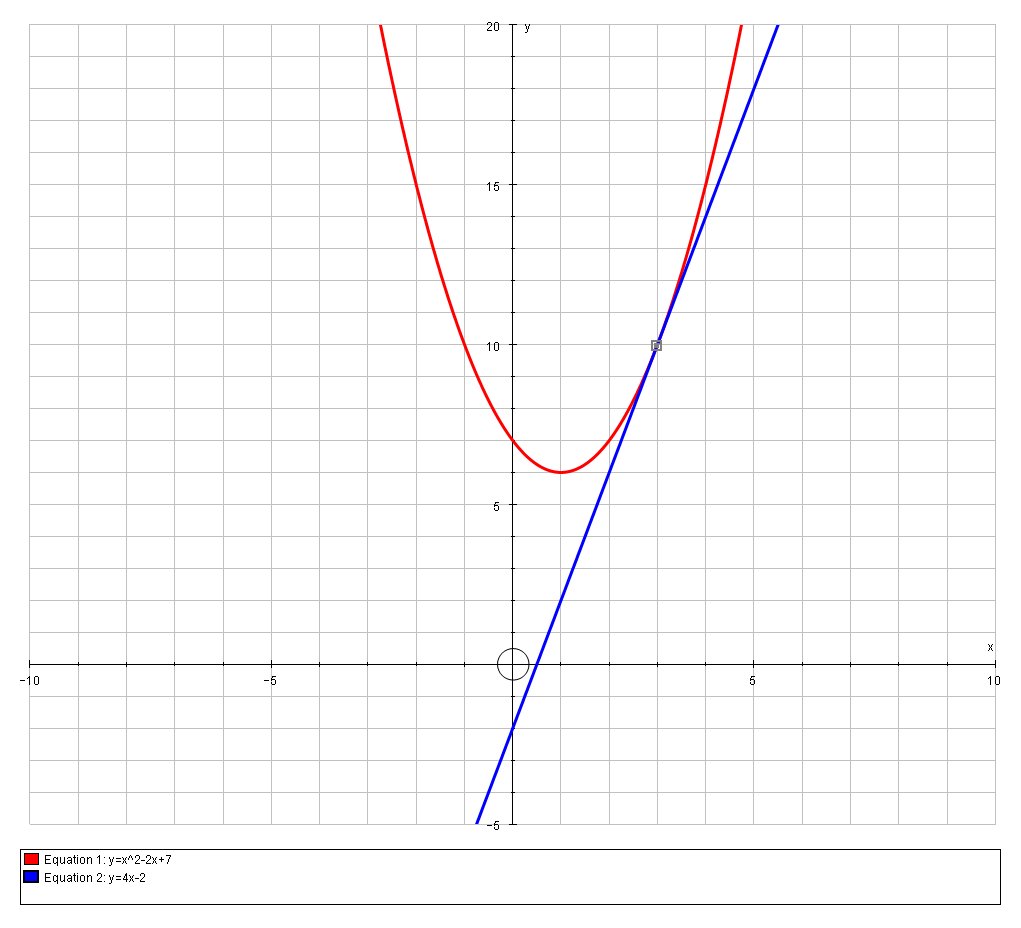 |
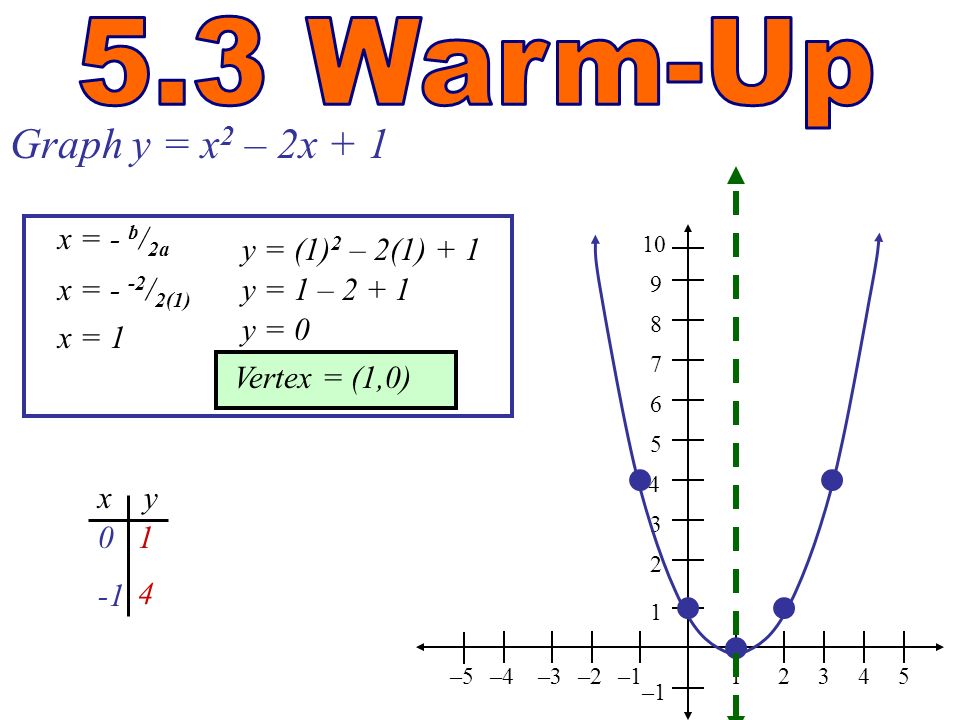 | ||
「Parabola y=x^2 1 y=19-(x)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
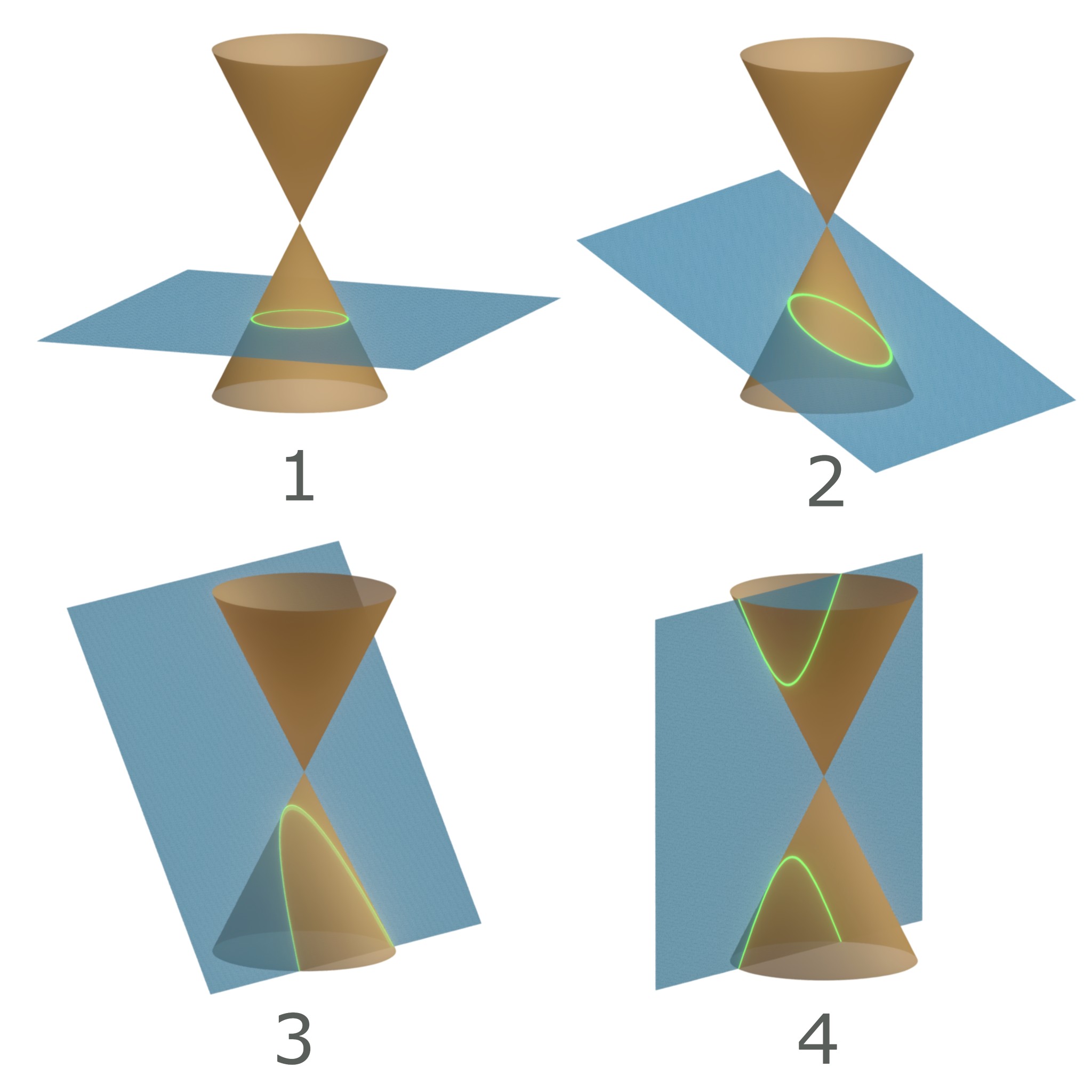 |  | |
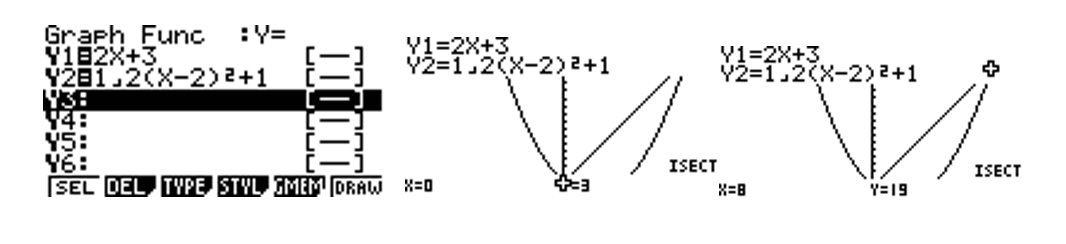 | 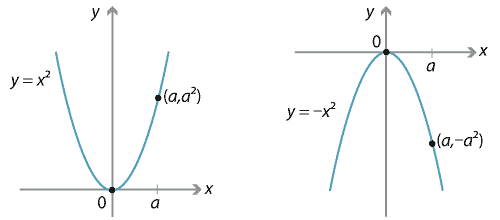 |  |
「Parabola y=x^2 1 y=19-(x)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
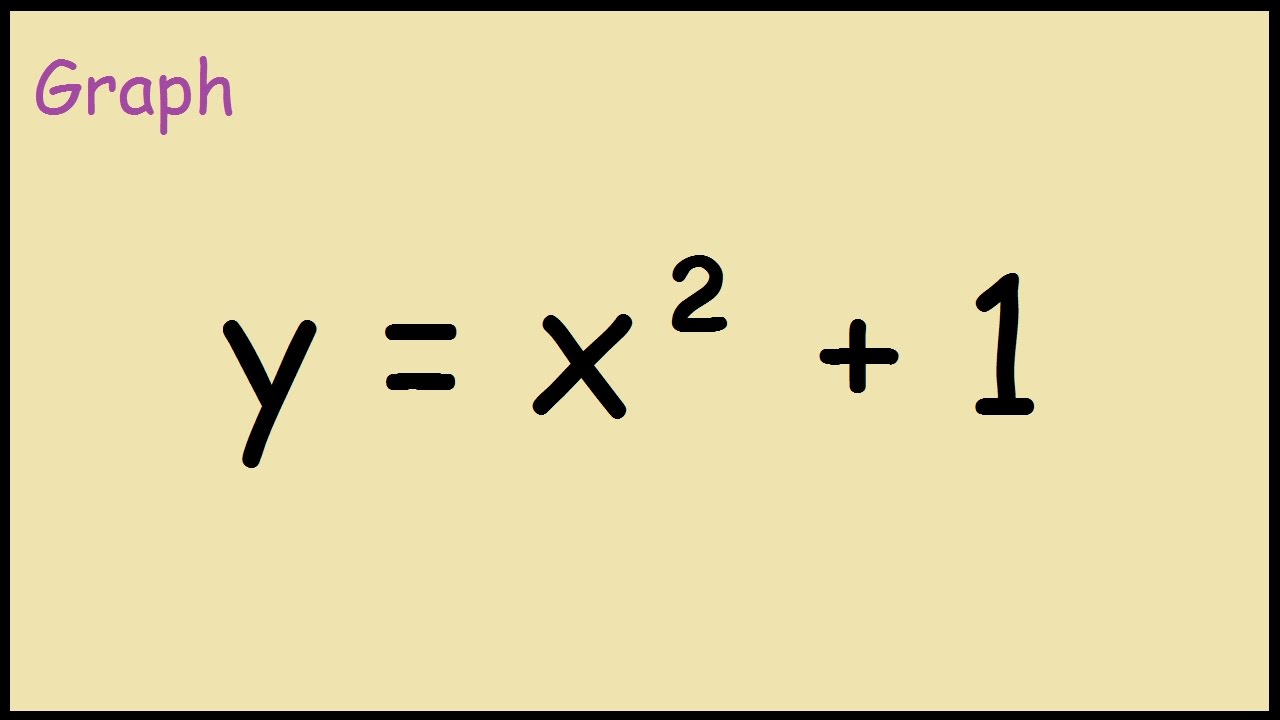 |  |  |
 | ||
 |  |  |
 |  |  |
「Parabola y=x^2 1 y=19-(x)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
The equation y " y ′ − 2 y = x 2 is called a differential equation because it involves an unknown function y and its derivatives y ′ and y " Find constant A, B, and C such that the function y = A x 2 B x C satisfies this equation (Differential equations will be studied in detail in Chapter 9) Clarissa N Numerade Educator Here is the question How to find the center of an osculating circle?
コメント
コメントを投稿